Look Here or Look Across
Introduction
Entity-Relationship (ER) Modeling is one of the essential topics covered in database courses. It aims to equip students with the necessary knowledge to transform business requirements into database schemas, which is a crucial step in database design.
One of the key aspects of ER modeling is understanding how to model cardinality constraints based on business requirements. For example, when designing a database to store employees’ information for a university, the business requirements might be:
- A person can be assigned to at most two departments at a time.
- For each assigned department, a person cannot work on more than one project.
- Every project must be associated with at least one department, with at least one person working on it.
It is important to ensure these constraints are enforced in the database, as it becomes difficult to enforce them once real data has been populated.
Correctly understanding cardinality constraints is critical. However, I have frequently encountered unclear cardinality constraints in ER diagrams drawn by students. Nine out of ten students fail to interpret them correctly, and the actual number may be even worse.
Why is that?
To my surprise, the issue is not that students don’t understand the concept. Rather, it’s because there are TWO interpretations of cardinality constraints in ER diagrams, and these two interpretations are EXACT OPPOSITES of each other! These conflicting interpretations are scattered randomly across the internet, so it’s no wonder students are confused.
Instructor to Student
Let’s assume we have two entity sets, Instructor and Student, and a relationship set advise. Suppose they form the following design, in which M indicates 1..* (many & total participation), and 1 indicates 1..1 (one & total participation).
How should we interpret the design? Is it many-to-one, or one-to-many?
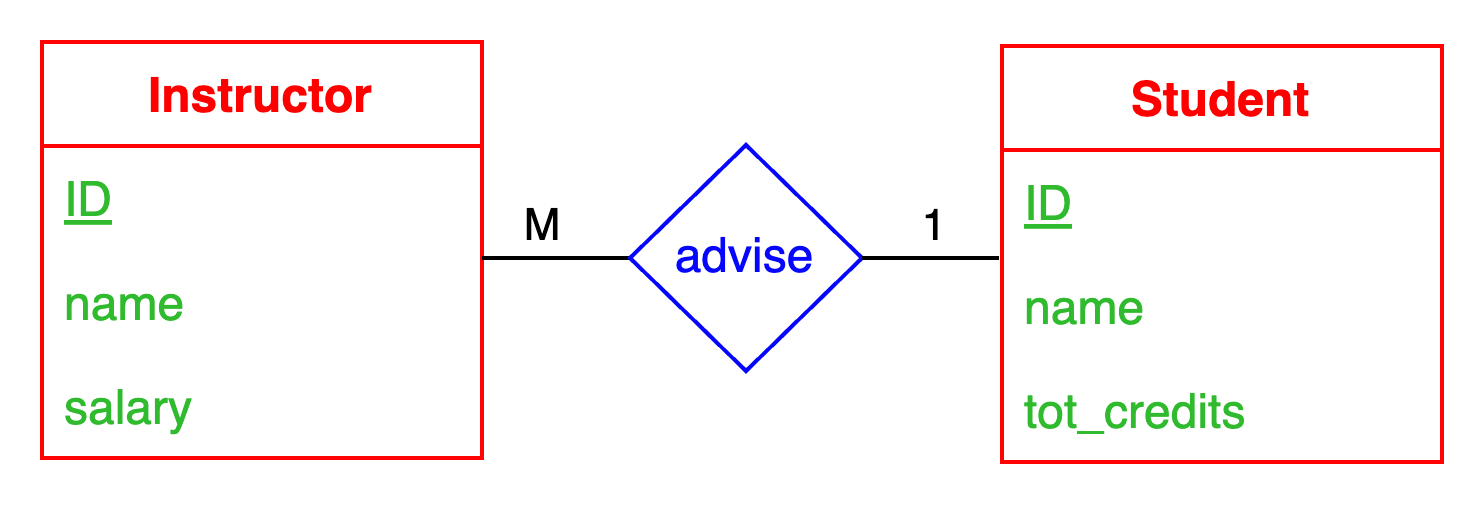
Many-to-One?
This interpretation is very intuitive since from left to right, the letters can be read as “M-to-1”.
But wait, the semantics seem confusing. Why can there be many (i.e., an unlimited number of) instructors who advise one student?
This interpretation does not make sense.
Well, if that interpretation is not correct, then should the correct interpretation be:
One-to-Many?
Entity-Relationship (ER) & Unified Modeling Language (UML)
ER, standing for Entity-Relationship, is a modeling technique proposed by Chen in 1976. It was first proposed as an alternative technique for modeling data, intended to be more intuitive than directly using the relational model. While people today often think in terms of relational models (such as SQL tables) for data management, ER modeling remains very useful design and is now the de facto standard for database schema.
UML, the Unified Modeling Language, proposed in 1990s, aims to provide a standardized way to visualize the design of systems, including structure, behavior, and interactions. While it is primarily used in object-oriented software development, UML is also commonly used for ER diagrams due to its similar way of representing entities, attributes, and relationships.
It’s not surprising that students often use UML tools to draw ER diagrams. However, this can lead to confusion due to differing interpretations of cardinality constraints. We’ll soon see why.
It is Many-to-One in UML or Chen’s ER
UML refers to cardinality constraints as association rules. In UML’s interpretation, the diagram above is many-to-one. This is intuitive.
Interestingly, this is also the interpretation in Chen’s ER model.
It is One-to-Many in the Textbook’s ER
However, in the ER model taught by textbooks like Database System Concepts, the interpretation is one-to-many.
The rationale is based on how ER diagrams are eventually translated into relational schemas. To make this translation more explicit, it helps to think this way:
- Each instructor can appear in
adviseup toMtimes; - Each student can appear in
adviseonly once.
The resulting relation, e.g., the Advise SQL table, would then look like this. Note that there must be no duplication, as it is a relational model:
| Instructor | Student |
|---|---|
| Instructor 1 | Student 1 |
| Instructor 1 | Student 2 |
| Instructor 1 | Student 3 |
| … | … |
This is the stage where we check whether the cardinality constraint is satisfied. Looking at the relational schema, it clearly reflects a one-to-many relationship.
Look Here or Look Across
This distinction remains important even when there is only the M shown.
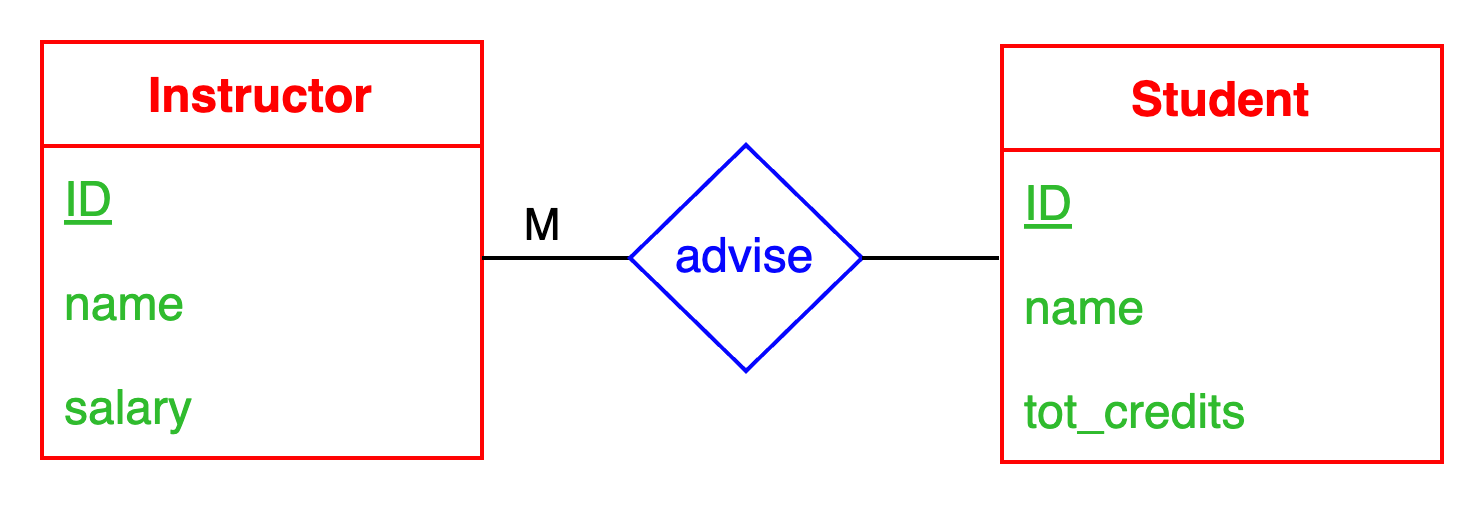
The M can be interpreted as:
- (UML or Chen’s ER): For each student, there can be up to
Minstructors - (Textbook’s ER): For each instructor, there can be up to
Mstudents
This is what people refer to as look here and look across. It is “look here” in UML because the M is read along with the entity set on the same side, Instructor in this case; It is “look across” in the textbook’s ER, because the M is interpreted relative to the entity set on the opposite side, Student.
N-ary Relationships
“Look here” and “look across” are two useful techniques for interpreting cardinality constraints. They can also be applied to N-ary relationships.
Assume we have the following diagram:
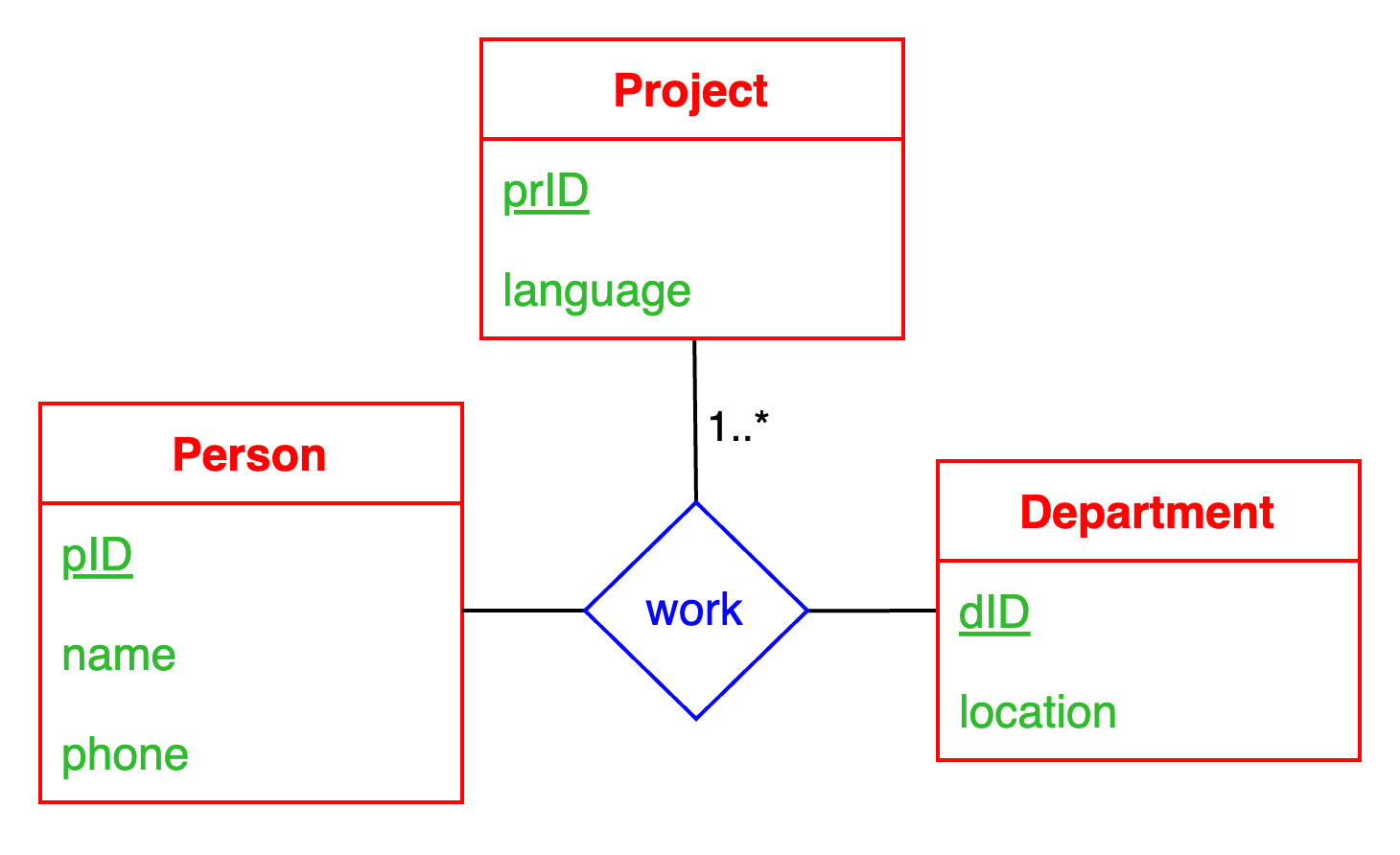
Then we interpret it as:
- (UML or Chen’s ER): For each (person, department) tuple, there can be many projects
- (Textbook’s ER): For each project, there can be many (person, department) tuples
Discussion
Referring to the cardinality constraints at the beginning of the post:
- A person can only be assigned to at most two departments at a time
- For each assigned department, a person cannot work on more than one project
- Every project must be associated with at least one department, with at least one person working on it
How do we represent these constraints using numbers on the diagram?
I’ll explain that in a future post.
If you found this useful, please cite this as:
Chen, Huanyi (Mar 2025). Look Here or Look Across. https://h365chen.github.io.
or as a BibTeX entry:
@article{chen2025look-here-or-look-across,
title = {Look Here or Look Across},
author = {Chen, Huanyi},
year = {2025},
month = {Mar},
url = {https://h365chen.github.io/blog/2025/Look-Here-Look-Across/}
}